Z-score berekenen met de Z-toets
De z-score of z-waarde geeft aan hoeveel standaarddeviaties een score van het gemiddelde af zit. Het is een verwachtingswaarde van een normale verdeling met een bekende standaardafwijking, uitgedrukt in eenheden van de standaardafwijking.
Hulp nodig bij je scriptie?
Vul je gegevens in voor een gratis en vrijblijvend adviesgesprek.
10.000+ studenten geslaagd
98% slaagt op tijd
Hbo & wo, online & offline
Scriptiebegeleiding sinds 2005
Inhoudsopgave
De z-score is een gestandaardiseerde waarde, zodat steekproeven uit verschillende populaties (mits voldaan wordt aan de aannames van parametrische toetsen) met elkaar vergelijken kunnen worden. Bijvoorbeeld, een z-score van 2 kan voor de ene variabele een waarde van 0,2 betekenen en voor de andere variabele een waarde van 10.001. Z-scores van 3 of extremer zijn erg zeldzaam (voor een normale verdeling is deze kans slechts 0,002). De verwachting van een z-score is altijd 0 met een standaardafwijking van 1.
Het belang van z-scores
Wat maken z-scores belangrijk? Wat heb je er aan? Ten eerste kun je aan de z-waarde, welke positief of negatief is, direct zien welke respondenten uit de steekproef boven en onder het gemiddelde zitten. Ten tweede is het mogelijk om scores op verschillende variabelen exact met elkaar te vergelijken, omdat de meeteenheid van de z-score gestandaardiseerd is. Tenslotte wordt de Z-verdeling ook wel de normale verdeling genoemd. Z-scores kun je namelijk makkelijk omzetten in oppervlaktes onder de normaal curve en dus weergeven als kansen of percentages. De vuistregel (de empirische regel) zegt namelijk dat in een normale verdeling…
- 68% van waarnemingen uit de populatie tussen een Z-score van -1 en 1 zit
- 95% een Z-score tussen -2 en 2 heeft
- 99,7% binnen 3 standaarddeviaties ten opzichte van het gemiddelde zit
Respondenten met een z-score groter dan 3 of kleiner dan -3 kun je dus meestal beschouwen als outliers (uitschieters). Deze principes van een normale verdeling gelden ook voor de Z-toets, bij het aantonen van significante verschillen. Onderstaande figuur geeft een visuele weergave van deze principes.
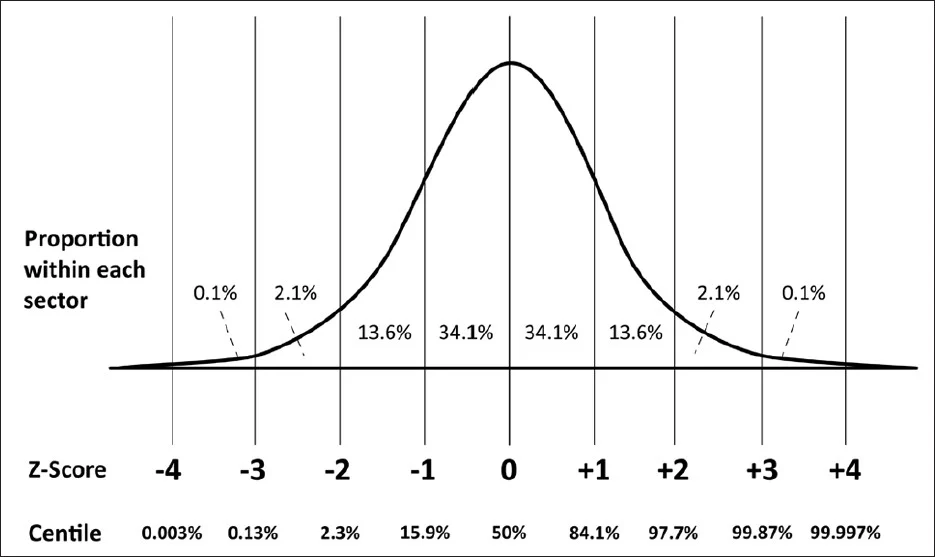
Z-score berekenen
De z-score wordt berekend met de z-toets. Dit gaat als volgt. Het gemiddelde van de dataset wordt aan 0 gelijkgesteld door elke score van het gemiddelde af te trekken. Deze uitkomst wordt gedeeld door de standaarddeviatie, zodat de standaarddeviatie gegarandeerd wordt gelijkgesteld aan 1.
De uitkomst hiervan noemen we een z-score of z-waarde. Deze berekening wordt weergegeven in de volgende formule:
Hier staat x voor een specifieke observatie, μ voor het gemiddelde van de populatie en σ voor de standaarddeviatie van de populatie. Als het gemiddelde en de standaarddeviatie in de populatie onbekend zijn, kunnen deze ook geschat worden aan de hand van een steekproef. Laten we een voorbeeld doornemen om dit te verhelderen. Stel dat 20 klasgenoten een tentamen hebben gemaakt. Hier hebben zij gemiddeld een 7 voor gehaald. De standaarddeviatie is 0,5. Sophie heeft een 6 gehaald. Wat is dan haar Z-score? Het invullen van de formule geeft dan: Z = (6-7)/0,5 = -2. Een Z-score van -2 betekent dat Sophie 2 keer 0,5 onder het gemiddelde zit.
De z-score tabel gebruiken
Met een z-score kun je in de standaard normale verdeling tabel opzoeken hoe (on)gebruikelijk deze score is. Deze tabel is ook te vinden in de bijlage van vrijwel elk zichzelf respecterend statistiekboek. In de linkerkolom zoek je de rij op die bij de betreffende z-sc0re (inclusief het eerste decimaal) hoort. Vervolgens zoek aan de bovenkant op basis van de tweede decimaal van de betreffende z-score de juiste kolom op. De cel waar de gevonden rij en kolom elkaar kruisen is het percentage van de populatie met dezelfde score of lager. Laten we een voorbeeld doornemen om het te verhelderen, op basis van bovenstaande voorbeeld van het tentamencijfer van Sophie. Haar cijfer heeft een z-score van -2. Je zoekt eerst -2 op in de tabel. Vervolgens zoek je bovenin het tweede decimaal op, in dit geval 0.00. In de cel waar deze twee getallen elkaar kruisen staat 0.0228. Dit betekent dat 0,0228% van Sophie’s klas (in dit geval de populatie) een cijfer heeft dat lager is dan zij of hetzelfde is als zij. Als je naar het figuur hier boven kijkt zie je inderdaad bij z-score -2 een percentage van 2.3%. In onderstaande figuur wordt dit nog eens geïllustreerd:

Let op: sommige standaard normale verdeling tabellen bevatten alleen positieve z-scores. Geen probleem. Om toch met een waarschijnlijkheidswaarde te vinden met een negatieve z-score maak je de volgende berekening: 1 – negatieve z-score. Een rekenvoorbeeld op basis van het voorbeeld van Sophie: 1 – 0,9772 = 0,0228. Easy does it!
Sneller afstuderen? Het maximale uit je scriptie halen?
Maak gebruik van de scriptiehulp van de ScriptieMaster. Meld je hier aan voor een gratis en vrijblijvend oriëntatiegesprek.
Heeft dit jou geholpen? Deel het met anderen:
Bekijk meer artikelen
Heb je vragen over dit artikel?
Laat een comment achter
Heb je vragen over dit artikel? Laat een comment achter en een van onze
begeleiders zal hem zo spoedig mogelijk beantwoorden
Wij bieden scriptiebegeleiding aan studenten van o.a.:
Inmiddels hebben onze scriptiebegeleiders van nagenoeg iedere vol- en deeltijd opleiding in Nederland studenten mogen ondersteunen bij hun afstudeertraject! Ben je nieuwsgierig geworden welke begeleider jou het beste kan ondersteunen bij jouw specifieke opleiding, studie en onderwerp? Vraag dan een gratis adviesgesprek aan. Hopelijk tot snel!




















